In the Spring of 2013, I took a research course on Computational Intelligence in Games as part of the Freshman Research Initiative program at UT. Recently, I was invited back by the professor to present as a guest speaker, showing off a project my partner and I started in the advanced course and have continued developing over the last few months. I say invited, because I ended up in class on the other side of campus while my partner presented to a room full of young, impressionable college freshmen. Nevertheless, the reception of our research was reportedly positive, and the first-year students were eager to ask questions about our motivations for the project, as well as implementation decisions regarding its structure.
But what was the project? Well, let’s back up a bit.
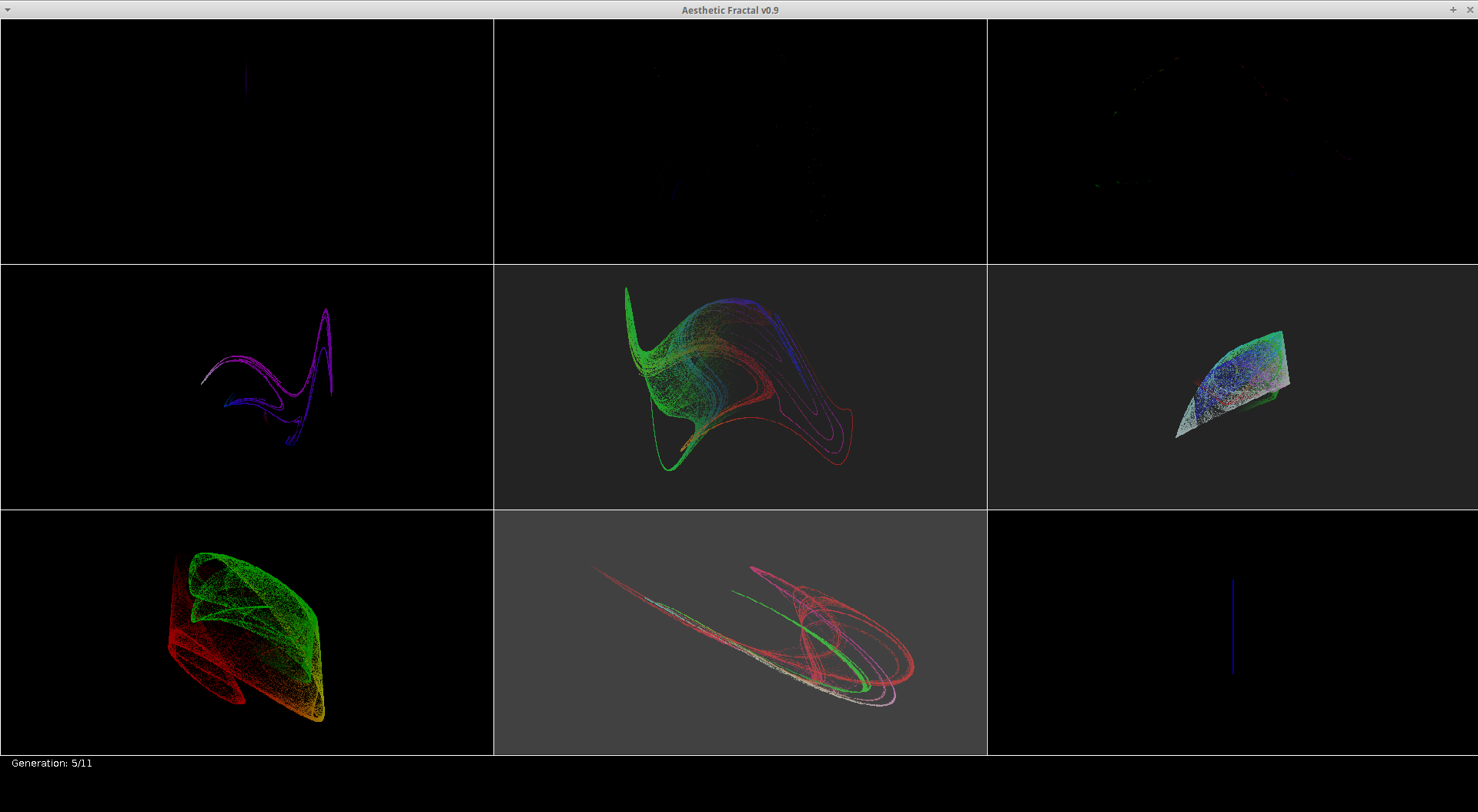
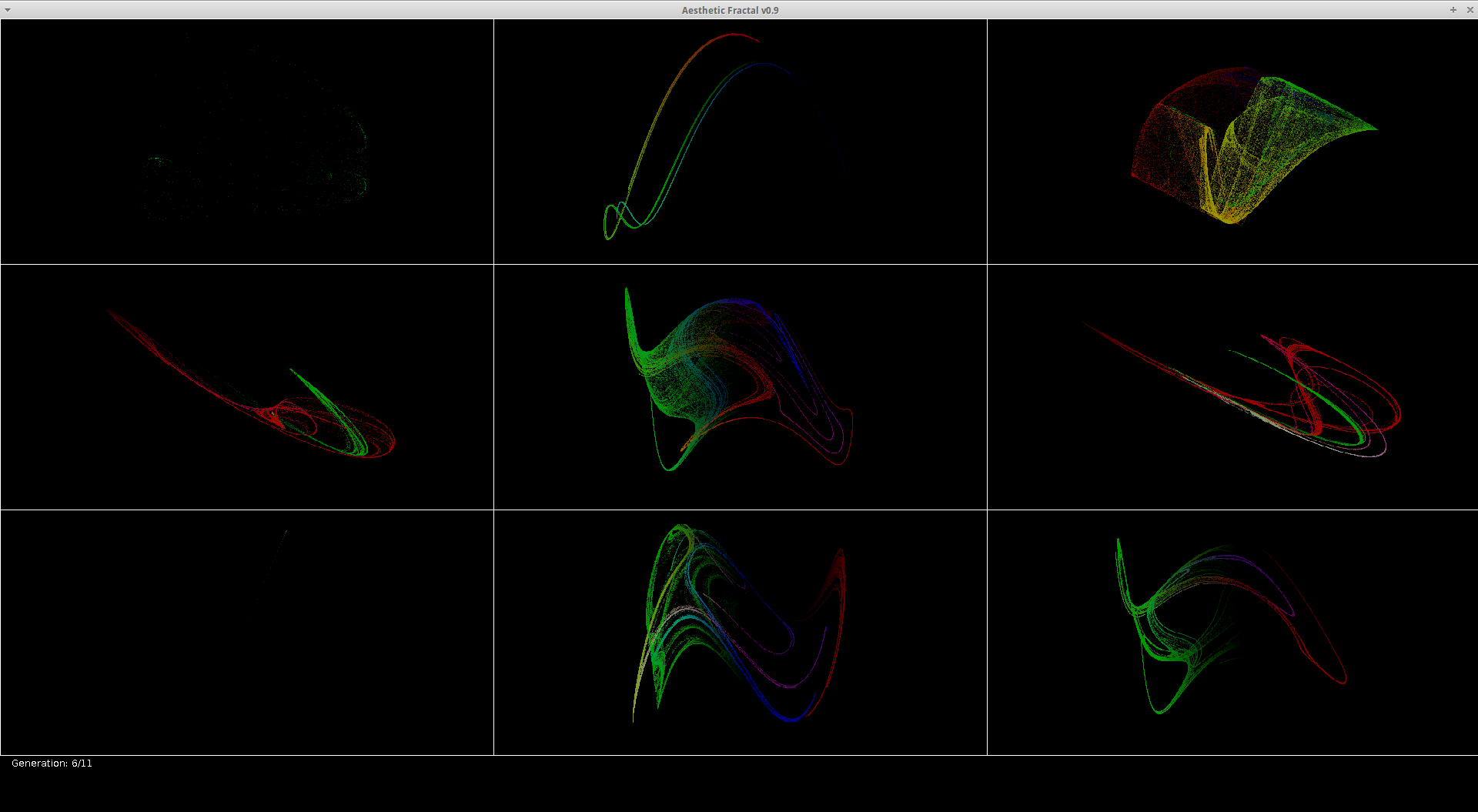
This is the current state of our research. In essence, it is an evolutionary fractal selector and part-time mating simulator. Tyler Yates and I starting building this system from scratch about six months ago, and we are finally starting to realize a smooth, efficient system for guiding the evolution of aesthetically-pleasing fractals. If you’ve ever had wet mathematical dreams of owning your own pet fractal, this is your chance to breed it.
We started off with a desire to correlate mathematical structures and subjective beauty, zoning in on a particularly simple and elegant family of fractals: the Clifford Attractor. Now, modifying constants is cool and all, but we’re looking for something bigger. Let’s see if we can’t evolve the structure of our fractals; to do that, we’re going to need a working knowledge of how our fractals are represented.
Fractals are all defined by the iterative evaluation of their equations, each of which describe how their XYZ position values and RGB color values will change over time in relation to previous evaluations. Our equations are parsed and represented as large expression trees with different types of nodes available for use: the most high-level types being terminals (values) and non-terminals (operators). One could imagine basic unary and binary operators like trigonometric and algebraic functions, but dream a little bigger and the possibilities start to flourish; start defining fractals in a programmatic way, and ternary if-then-else nodes become possible, integrating conditional behaviors into a visual medium.
With each operator and value incorporated into its own node, it’s easy to see how one could start evolving equations. There are three basic methods of evolution that we use to create new equations for fractal children: cross-over along operators, mutation along constants, and introduction. These three methods serve different purposes in the grand scheme of making fractal babies, all of which are important in generating a wide variety of possible fractals that could be pleasing to the user at hand.
Mutation along constants is the safest of the evolutionary methods; the equation form is kept intact, and constants are modified by a small, random displacement. The result is a fractal that holds the same iterative behavior, with accentuation on certain curvatures of its shape.
Cross-over involves two equations; a subtree is chosen from each fractal and swapped, generating an entirely new equation form. The resulting fractal, therefore, belongs to a separate family of fractals that, while having similarities with the previous family, will have a modified iterative behavior.
Finally, Introduction ings new operations into the fold. Things like absolute values, tangents, and conditionals can be inserted into the expression tree, modifying behaviors and inging with it the most uncertainty out of our three methods. This is the wildcard of the bunch, taking the equation form in new directions.
With these evolutionary methods, users start tending towards fractals with certain shapes that are pleasing to their own personal taste; but how varied can these fractals get, and how many are truly interesting?
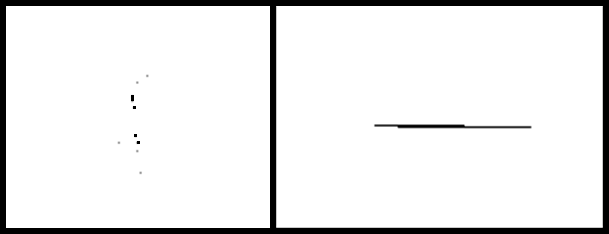
This is a sparse fractal. We define a sparse fractal to be one whose visual representation is aesthetically unappealing due to its lack of density or form, like specks of paint on a large canvas. We incorporate a number of varied operations in our system, all of which can be introduced repeatedly and combined haphazardly; the consequence of our mayhem is the enormous sample space for our fractals, which makes sparse fractals a near certainty. In fact, we observed 10 generations of fractals in our program and found 80% of them to be what we considered sparse fractals.
In approaching the problem of filtering, we established two criteria on what constitutes a non-sparse fractal:
- A sufficiently large number of distinct points
- The presence of non-linear figures (e.g. curves)
In explaining our thought process for filtering, Tyler says it best:
"Initially, our first approach was to create a set of point objects representing all the distinct pixels drawn on the fractal's image. The final size of the set after all points had been drawn was then used to determine if the fractal was sparse or not. This method worked well for determining the first criterion because all that is needed is a numeric threshold for determining the minimum number of distinct points in a non-sparse fractal. This method was not very useful in determining the second criterion however as there was no efficient way to determine the linearity of the figure from just the set of points. </br></br> Our next approach was to divide the image into square regions and count how many regions the fractal intersected. This method worked well for determining the second criterion as curves would intersect more regions than a straight line. Determining the first criterion however was difficult as a sparse fractal could have few points but still intersect many regions if the points were far enough apart. </br></br> The final method we devised was able to determine both criterion with a high rate of success and did not require much computation. Rather than look at the individual pixels in the image of a fractal, the program looks at the image file itself, specifically at how large the image file is in bytes. To understand this methodology, we need to describe the format of the images created by the program. </br></br> Our program uses the PNG image format for saving images of the generated fractals. PNG is a lossless image format, meaning no data is lost when saving the image (compare this to the JPG image format where data can be lost for the sake of smaller image sizes). Thus, the only way PNG encoders can reduce the sizes the output file is to perform lossless compression techniques. One technique that PNG encoders use is to find large regions of one color and reduce that region to a single block of information in the output. This technique works remarkably well for reducing the sizes of images that are composed only of lines because the encoder only needs to save the endpoints of each line in the output file. This compression technique also works well for images that have very few points that are different in color than the background as only a few points need to be saved in the output. </br></br> Thus, PNG encoders are able to compress sparse fractal images very well because they are well suited to the lossless compression algorithms used in encoding PNG images. Exploiting this fact, we were able to define a size threshold for the PNG files of sparse fractals. For fractals rendered at a resolution of 640x360 pixels we defined the cutoff as 1 kilobyte, such that any fractal whose PNG file was smaller than this cutoff was marked as sparse. Thus, any fractal whose image file has a size of less than 1 kilobyte is marked as sparse and is not shown to the user. Instead, a new fractal is generated to replace it. Through manual testing we have found that this size threshold has a high rate of success for correctly determining the sparsity of a fractal."
Great! Now we have a system for generating and evolving fractals in a large, vast sample space, and we don’t have to deal with all the junk to get there. It works well, it works fast, you can go back into your history and retry generations, you can save your entire family history and load them up in an instant. But you can’t appreciate your fractals. Your fractal takes up, at best, 1/9th of your screen, they’re drawn with a small number of points to expedite the evolution process, and you can’t tweak them to your liking. What did we come all this way for?
…oh? Hello, beautiful.

Your very own OpenGL Renderer. 360-Degree rotations. Infinite zoom. Millions of points for precision curvature. Every equation that defines your fractal, right there in your fingertips. In full-screen, HD-resolution glory.
Groom your fractal. Feed it a nice background color. Take a snapshot and share it with your friends. Save it for prosperity.
Your very own fractal family.